Model definitions¶
Both Neural Network Inputs as well as the Model Kinetics of the mechanistic part are set via smart equation editors that provide access to variables, mathematical operators and functions.
Note
For specific examples on how to set up the (hybrid, neural network, mechanistic) model, see the quick start guides.
Note
Output variables (displayed in green once selected) can be used as neural network model Neural Network Inputs if the model (at time \(t\)) should depend on its previous (timepoint \(t-1\)) output value.
Input variables are colored in purple once selected.
- The equation editors allow to
use individual variables, e.g.
Var_A,use multiple variables in a single expression, e.g.
(Var_A + Var_B) / Var_C,use basic mathematical operators such as
+Addition, which computes the sum of its operands.-Subtraction, which subtracts its right-hand operand from its left-hand operand.*Multiplication, which computes the product of its operands and/Division, which divides its left-hand operand by its right-hand operand.
apply simple mathematical functions, e.g.
Var_A + sqrt(Var_B/Var_C). Available functions areabs()Absolute, which returns the absolute value of a specified number,sqrt()Square root, which returns the square root of a specified number,^. Power, which returns a specified number raised to the specified power. E.g.(5)^(3) = 125.exp()Exponential, which returns Euler’s number \(e\) raised to the specified power,ln()Logarithm, which returns the natural (base \(e\)) logarithm of a specified number,sin()Sine, which returns the sine of an angle measured in radians andcos()Cosine, which returns the cosine of an angle measured in radians.
Use parenthesis
(,)for grouping.
Neural Network Inputs¶
Inputs for the neural network (either plain variables or more or less complex mathematical expressions) can be set in this dialog by using the + button (Add a new definition) in the right upper corner, clicking in the corresponding Definition field and entering the desired expression. Typically, online sensor data available at a high frequency will be used here.
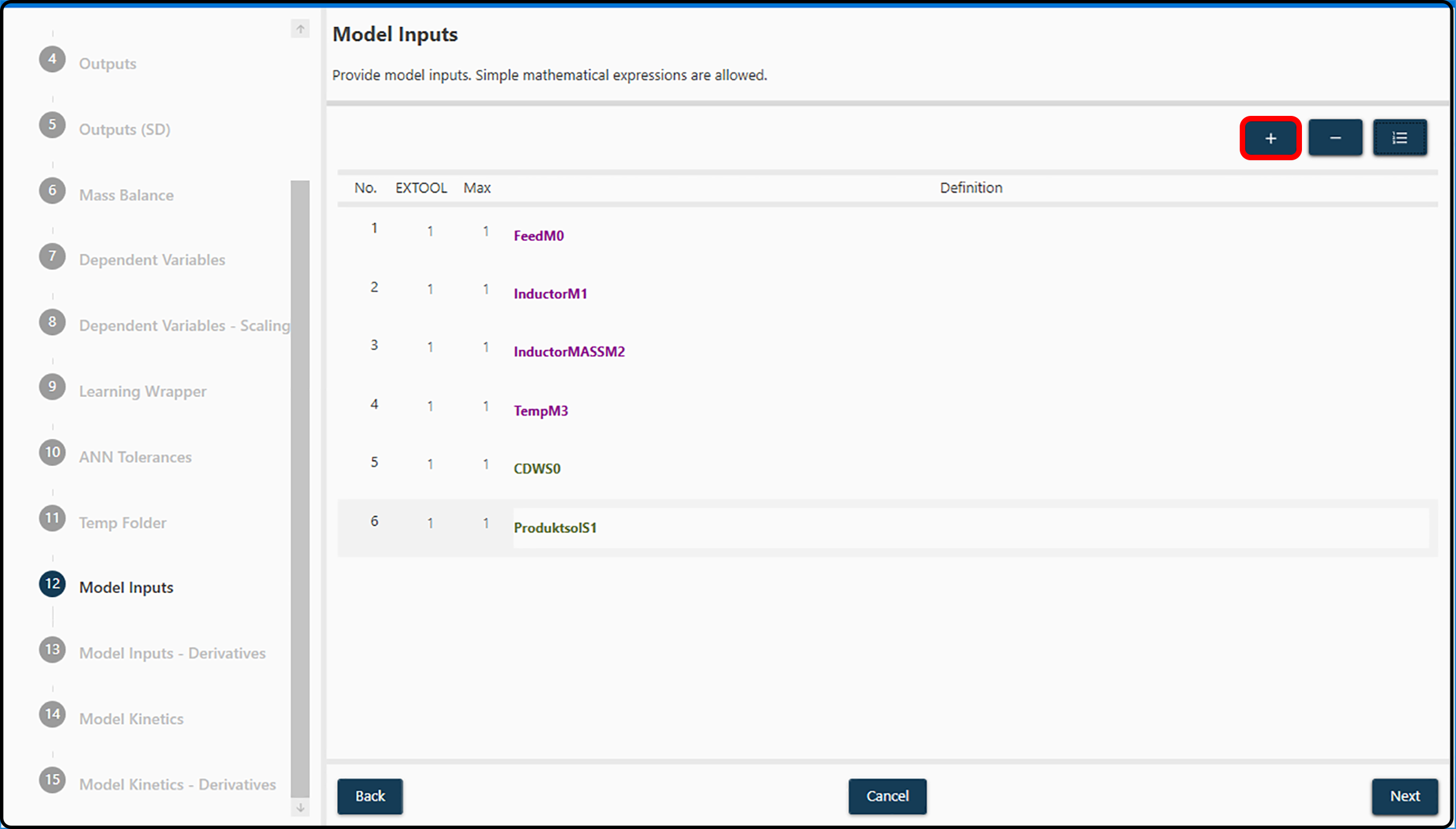
Figure 23. Definition of model inputs via the smart equation editor. New variables/expressions are added with the + button marked in red.¶
Possible actions are,
Add. Definitions can be added by clicking Add a new definition,
Remove. Definitions can be removed by selecting and clicking Remove selected definition and
Refresh Names. If multiple definitions are added and deleted or their order is modified, by clicking the Update definition index, input names and indices are reordered and renamed.
Example
Consider the following definition of input and output variables:
Output variables names are,
Var_Out_1,Var_Out_2,Var_Out_3.Input variables names are,
Var_In_1,Var_In_2,Var_In_3,Var_In_4,Var_In_5.
Case 1: If we know that the model doesn’t depend on its previous output values; depends on Var_In_1, the natural logarithm of Var_In_4, and its Var_In_2 / Var_In_3 ratio,
The following input definitions were appropriate,
IN 1:
Var_In_1IN 2:
ln(Var_In_4)IN 3:
Var_In_2 / Var_In_3
Case 2: The same scenario as in Case 1 but now we know that the model depends on its previous output values, particularly on Var_Out_2 and the Var_Out_3 / Var_Out_1 ratio.
Now we would update our input definitions to,
IN 1:
Var_In_1IN 2:
ln(Var_In_4)IN 3:
Var_In_2 / Var_In_3IN 4:
Var_Out_2IN 5:
Var_Out_3 / Var_Out_1
Note
When adding input definitions and clicking in the Definitions field, a list of available variables (and expressions) becomes visible. Compared to their original names, output/state variables have an appended S + a number, while several other inputs have an appended M + a number. The reasons are only of technical nature and shall not be of any concern.
Once all inputs for the neural network model are entered and the Next button is pressed, the user is guided to the Model Kinetics dialog.
Model Kinetics¶
Similar to the neural network model definitions, the kinetic definitions can vary from a single variable assignment to complex mathematical expressions. The kinetics are used to connect the outputs of the ANN with the overal model outputs.
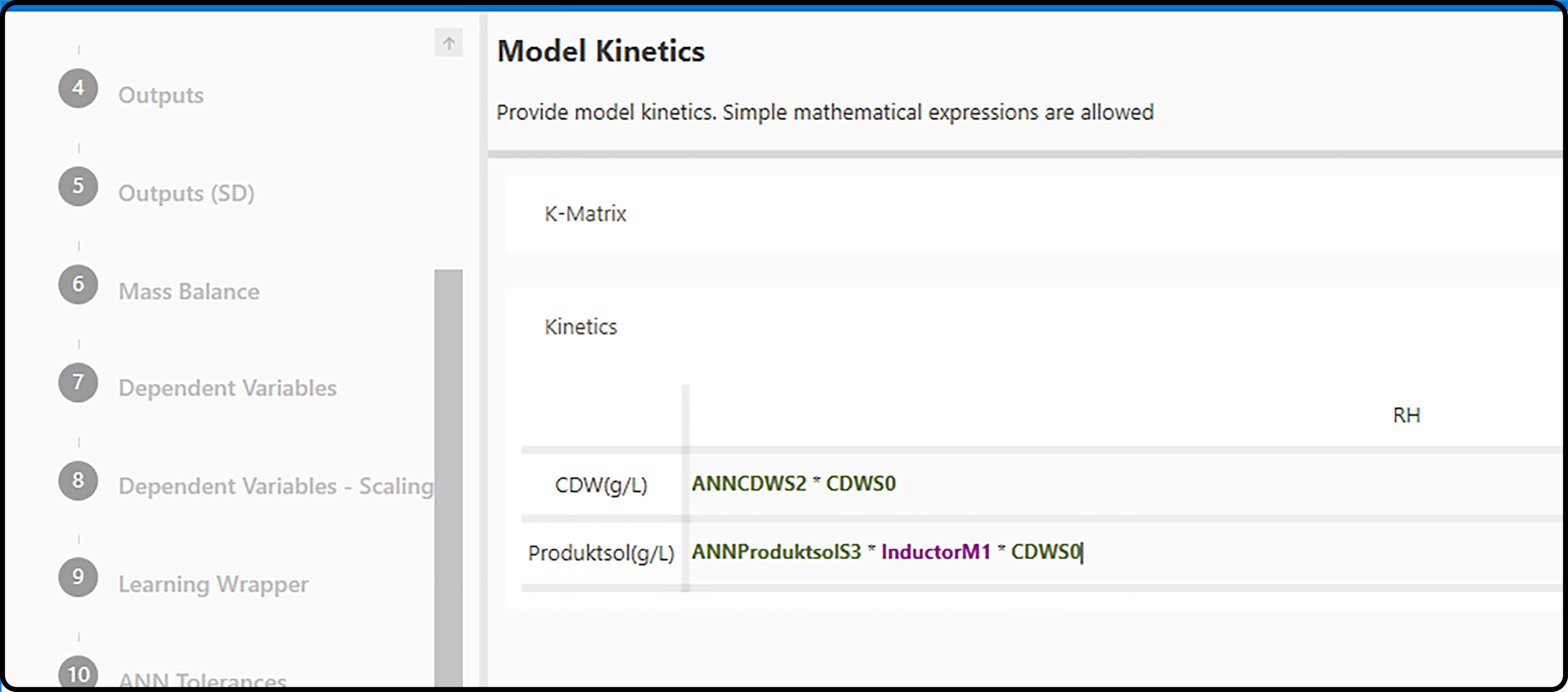
Figure 24. Definition of the model kinetics via the smart equation editor.¶
Note
Unlike the neural network model definitions, not only input and output variables can be used in the kinetic expressions, but also the outputs of the neural network. These variables have an ANN prefix.
Example
Consider a situation with \(5\) input and \(3\) output variables and therefore also \(3\) outputs of the neural network:
Output variables names are,
Var_Out_1,Var_Out_2,Var_Out_3.Input variables names are,
Var_In_1,Var_In_2,Var_In_3,Var_In_4,Var_In_5.Model outputs names are,
ANNVar_Out_1,ANNVar_Out_2,ANNVar_Out_3.
Case 1: Assume that no extra kinetics are required. In this scenario the overall model outputs can be defined as the direct output of the neural network:
RH Var_Out_1:
ANNVar_Out_1RH Var_Out_2:
ANNVar_Out_2RH Var_Out_3:
ANNVar_Out_3
where the left side RH Var_Out_x represents the current (\(t_i\)) model Var_Out_x output.
Case 2: Assume kinetics are required and the neural network outputs act as rates of the previous model outputs. The kinetics can be defined as,
RH Var_Out_1:
ANNVar_Out_1 * Var_Out_1RH Var_Out_2:
ANNVar_Out_2 * Var_Out_2RH Var_Out_3:
ANNVar_Out_3 * Var_Out_3
where the left side RH Var_Out_x represents the current (\(t_i\)) model Var_Out_x output and the right side Var_Out_x is the model output at the previous iteration (time \(t_i - 1\)).
Important
The kinetics definitions (differential equations) can be set as needed by using as many of the available variables, operators and functions. Previous cases are just very simple examples and more complex expressions are possible,
e.g.
RH Var_Out_3:
ANNVar_Out_3 * Var_Out_3 * (1/sqrt(ANNVar_Out_2)).
Note
For a specific example on how to set up the mechanistic part of the hybrid model (the kinetics), see the quick start guides.
Fitting the hybrid model¶
Once all model definitions are completed, the hybrid model can be calculated using the Start button in the left upper corner.

Note
In the lower/middle part of the window all parameters of the current model can be found: learning wrapper, model inputs, kinetics, datasets and further parameters. After model calculation via Start, the Reset button can be used to have access to these parameters for possible changes and recalculation of the hybrid model.